Looking behind the software

Over six years have passed since BSJ reported on the results and issues raised in the International Energy Agencies Annex 21 'Empirical validation of thermal building simulation programs using test room data'.

To some, the results of the investigation were surprising and worrying. For others it was nothing new. A few had already understood that modelling, no matter how complex, could never truly capture the real physics of, say, transient multi-dimensional heat transfer subject to turbulent boundary flow.

Fortunately it would be impossible to 'uninvent' modelling and simulation applicable to building services engineering. Although issues were raised in Annex 21 about the ability of the numerical tools to predict the internal temperature and energy consumption of simple test cells, it is difficult to see what other techniques could replace or better them.

Couple this with the current emphasis on increased energy efficiency and sustainability and we now have a need for better understanding of the physics of complex building heat transfers. These are clearly areas the simulation tools could help to resolve.

Six years on and a trawl of the relevant literature will show a healthy and possibly growing application of dynamic thermal modelling (dtm) and computational fluid dynamics (cfd) to building services engineering oriented problems.

Modelling for beginners
While many in the industry appear to have accepted the necessity for modelling it is not obvious how newcomers to the field gain an understanding of the relevant computational procedures.

Computational tools are becoming more useable with the coupling of the solver routines to high quality user interfaces. Today's user interacts with the software not by giving 'command lines' but by setting switches or clicking buttons in dialog boxes or menus.

It is, however, possible that this greater usability may create a potential conflict for the simulation sector. This 'point and click' facility may hide too much of the underlying procedures of the methodology being used. It is a delicate balance that modern commercial software developers and vendors have to assess. If the software is too simple, the tools can be used by inexperienced operators which may lead to problems with the quality of the predictions. Such poor quality predictions, possibly more a function of the inexperienced user rather than the code itself, will only lead to an increase in the criticism levelled at the tools. For the vendors, therefore, this problem is without doubt a double-edged sword.

However useable the code the analysts should, it is argued, still be in a good command of the detail that is embodied in modern cfd and dtm solvers. Greater usability should not detract from this fundamental necessity.

To help in this area and to give the undergraduates at the University of Hertfordshire experience of numerical modelling, a finite difference solver has been developed. The solver is currently configured to study the two-dimensional transient conduction equation (see graphic, 'Two-dimensional transient conduction equation').

The choice being made on the grounds of:

• It is non-trivial ie the code is two-dimensional and transient.
  
• It is not overly complex. It does not include three dimensions nor convective transport.
  
• The relevant physics of the maths surrounding the problem should be understood by today's undergraduates.
  
• It will allow real, interesting building services engineering problems to be studied.
  
• Some of the generic numerical analysis issues relevant to both dtm and cfd can be studied.

The code, FDiff3, currently allows the user to describe the following boundary conditions (see graphic, 'FDiff3 boundary conditions').

All of which could be set differently for both a steady and transient analysis.

The code has also been written to allow the user to describe different local areas within the domain. These areas could have, for instance:

• a local heat source;
  
• a local fixed temperature;
  
• local material properties.

Practical implementation
While the coding of the above source terms into the equation is an interesting challenge in its own right, the practical implementation of these terms might be more relevant to building services engineering undergraduates.

For these local source terms could be used to help study, say, the performance of a concrete slab with an embedded hot or cold coil ie an underfloor heating or cooling system or by changing the local material properties the user can also study heat bridging within a parent material. All of which are important areas within thermal modelling.

FDiff3 is written in Visual C++ and hence has the usual interface components that is expected of modern computer programs but, in line with the approach undertaken by its author, it does not hide all the internal switches.

For instance, in a transient calculation of heat transfer there is a need to describe to the code a fixed time increment. In the explicit procedure there is a stability limit placed on this time step whereas in the implicit procedure there is not. In the explicit procedure of FDiff3, the code calculates the maximum time step but does not apply this value blindly. The user is free to select this value or apply their own time increment. This way the code helps the users start to develop an understanding of some of the issues surrounding the choice of an appropriate time step.

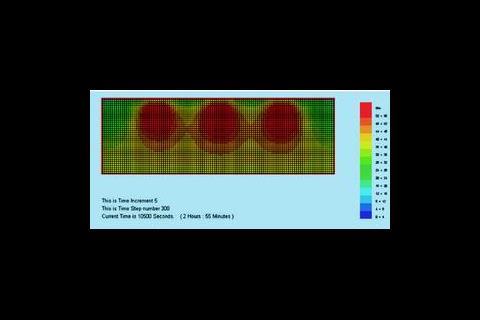
To elaborate on this point the output from FDiff3 of two separate studies on a two-dimensional slab with three embedded heat sources is shown on the previous page. In figure 1a the results were obtained using a time increment of 35 seconds, whereas in figure 1b the results were obtained using a time increment of 35·4 seconds. For both cases the maximum time step for stability has been calculated at 35·4 seconds.

Note at the top of figure 1b the 'checker box' temperature profile between neighbouring cells. For this type of problem, this behaviour typifies an unstable – oscillating solution.

For our final year students the open nature of the source code is such that they are encouraged to develop their own routines to implement in the parent FDiff3 solver. Again helping to developing both their understanding of a generic numerical code and the functions used to arrive at predictions. The intention here is to increase their competence when using and applying commercial codes to study real building services engineering problems.

User or understander?
As stated in our CIBSE National Conference 2002 Poster the difference between 'users' and 'understanders' may be a subtle one but it is an important one. Pushing buttons to use code is not understanding the methodology. The approach we apply to our undergraduates will, it is hoped, help them to better understand the issues and the underlying procedures behind the buttons they have just pressed.

For while we are not promoting Code A over Code B we are, using FDiff3, helping to develop the students' understanding of the generic features that are likely to be embodied in both Code A and Code B.

For instance FDiff3 currently allows such studies of mesh dependency, influence of boundary conditions, implementations of different internal source terms and the study of heat bridging. Stability issues, or issues surrounding different numerical schemes and different solution schemes (direct and indirect) can also be studied with this code (all generic numerical analysis issues).

Post processing is also undertaken by FDiff3, and for transient problems, the code is provided with an ability to animate the results at each saved time step.

This animation facility is an important one in its own right as it helps to show the temporal as well as the spatial distribution of temperature through two-dimensional domains. Should the students wish to use commercial post-processing programs the code also outputs data suitable for reading by the Fieldview¹ post processor.

Although the diffusive nature of the conductive process can be seen from figures 2a to 2d, the animated routines, which are not possible to be shown here, provide the user with a real feel for the temporal behaviour of the diffusive process.

Conclusion
Many of the codes used during the IEA study employed numerical analysis techniques. Such techniques are well founded in mathematics in helping resolve differential equations ie the type of equations that best describe the physics of the problems studied during the IEA study.

The essence of numerical analysis, (which is embodied in both computational fluid dynamics and dynamic thermal modelling), is the re-casting of the governing differential equations into a set of algebraic relationships. These relationships are then converted into routines suitable for computational solution.

FDiff3 gives the students an open and safe opportunity to use a numerical heat transfer solver to both help them better understand the physics of transient heat transfer and the subject of numerical modelling.

This is essential if we are to truly continue with the quest to develop low energy buildings using the sophisticated modelling tools in a robust manner.